Next: Hőmérsékleti teljesítményspektrum Up: A kozmikus mikrohullámú háttérsugárzás Previous: A foton- és neutrínóeloszlások
A ![]() hőmérsékleti fluktuáció
hőmérsékleti fluktuáció
![]() Fourier-transzformá
ltjára vonatkozó Boltzmann-egyenlet a
Fourier-transzformá
ltjára vonatkozó Boltzmann-egyenlet a
![]() hullámszám-vektor
hullámszám-vektor
![]() irányától csak a
irányától csak a
![]() skalárszorzaton keresztül függ [37],
így
skalárszorzaton keresztül függ [37],
így
![]() kifejthető a
kifejthető a
![]() Legendre-polinomok szerint:
Legendre-polinomok szerint:
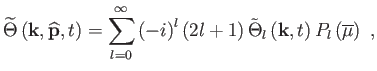 |
(6.119) |
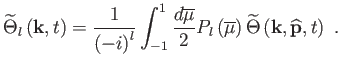 |
(6.120) |
A fenti egyenletrendszer önmagában még nem határozza meg a multipólusok fejlődését, szükséges hozzávenni a
![]() és
és
![]() Bardeen-potenciálok fejlődésegyenleteit (ezeket a (6.86)-(6.87)
Einstein-egyenletek adják). Utóbbiak viszont összecsatolódnak a
neutrínókra, a barionikus- és a sötét anyagra vonatkozó fejlődésegyenletekkel is.
Bardeen-potenciálok fejlődésegyenleteit (ezeket a (6.86)-(6.87)
Einstein-egyenletek adják). Utóbbiak viszont összecsatolódnak a
neutrínókra, a barionikus- és a sötét anyagra vonatkozó fejlődésegyenletekkel is.
A neutrínó-eloszlásfüggvényt jellemző
![]() perturbációra ugyanazok érvényesek, mint
perturbációra ugyanazok érvényesek, mint ![]() -ra, azzal a kivétellel, hogy nincs szórási tag. Az
-ra, azzal a kivétellel, hogy nincs szórási tag. Az
![]() momentumok fejlődésegyenleteit (6.121)-(6.124) egyenletek adják
momentumok fejlődésegyenleteit (6.121)-(6.124) egyenletek adják
![]() -val és végrehajtva a
-val és végrehajtva a
![]() cseréket.
cseréket.
A fotonokon és neutrínókon kívül a többi anyag (barionok, hideg sötét anyag) komponens nemrelativisztikus. Ez ahhoz vezet, hogy a barionok és a hideg sötét anyag perturbált eloszlásfüggvényei első két momentumához (energiasűrűség- és sebességperturbációk), képest a magasabbak elhanyagolhatók.
A teljes egyenletrendszer megtalálható [12] forrásban, numerikus megoldása megadja a CMB-multipólusok időfejlődését. A kezdeti feltételek adiabatikusak, teljesítik többek között a
Szeged 2013-05-01