Next: A hőmérsékleti teljesítményspektrumot meghatározó Up: A kozmikus mikrohullámú háttérsugárzás Previous: A hőmérsékleti fluktuáció Fourier-transzformáltjának
A ![]() hőmérsékleti fluktuációt véletlen valószínűségi mezőként kezeljük.
Valószínűségi mezők esetén cél az eloszlásfüggvényük minél
pontosabb
meghatározása. Az eloszlásfüggvény meghatározható tetszőleges
számú pont
korrelációs függvényei ismeretében. Gauss-valószínűségi mező
esetén a tetszőleges számú pontkorrelációs függvények
visszavezethetők 2-pont korrelációsakra (Wick-tétel),
ezért elegendő ez utóbbiak meghatározása.
hőmérsékleti fluktuációt véletlen valószínűségi mezőként kezeljük.
Valószínűségi mezők esetén cél az eloszlásfüggvényük minél
pontosabb
meghatározása. Az eloszlásfüggvény meghatározható tetszőleges
számú pont
korrelációs függvényei ismeretében. Gauss-valószínűségi mező
esetén a tetszőleges számú pontkorrelációs függvények
visszavezethetők 2-pont korrelációsakra (Wick-tétel),
ezért elegendő ez utóbbiak meghatározása.
Feltesszük, hogy a ![]() hőmérsékleti fluktuáció Gauss-valószínűségi
változó, ami a FLRW háttér szimmetriáival összhangban
statisztikailag homogén és izotrop. A statisztikai homogenitás és
izotrópia azt jelenti, hogy a
2-pont-korrelációs függvény invariáns a térbeli eltolásokkal és
pont körüli
forgatásokkal szemben.
hőmérsékleti fluktuáció Gauss-valószínűségi
változó, ami a FLRW háttér szimmetriáival összhangban
statisztikailag homogén és izotrop. A statisztikai homogenitás és
izotrópia azt jelenti, hogy a
2-pont-korrelációs függvény invariáns a térbeli eltolásokkal és
pont körüli
forgatásokkal szemben.
A hőmérsékleti fluktuációt adott helyen és időben (
![]() és
és ![]() rögzített) mint irányfüggő (
rögzített) mint irányfüggő (
![]() -tól függő) mennyiséget
figyeljük meg. Az egységgömbön a gömbharmonikusok ortonormális
bázist
alkotnak, így a megfigyelt
-tól függő) mennyiséget
figyeljük meg. Az egységgömbön a gömbharmonikusok ortonormális
bázist
alkotnak, így a megfigyelt
![]() hőmérsékleti
anizotrópia mezőt alkalmas kifejteni ezen bázis szerint:
hőmérsékleti
anizotrópia mezőt alkalmas kifejteni ezen bázis szerint:
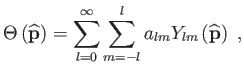 |
(6.128) |
A 2-pont korreláció Legendre-együtthatói megadhatók az ![]() gömbfüggvény-együtthatók
gömbfüggvény-együtthatók
![]() korrelációjával is. Felhasználva a
gömbfüggvények addíciós tételét, a statisztikai izotrópia miatt:
korrelációjával is. Felhasználva a
gömbfüggvények addíciós tételét, a statisztikai izotrópia miatt:
A
![]() valószínűségi változók amplitúdói és fázisai függenek a kezdeti
perturbációktól. A hőmérsékleti fluktuációra vonatkozó (6.121)-(6.124) Boltzmann-egyenlet
multipólus-komponensek azonban
nem függnek expliciten
valószínűségi változók amplitúdói és fázisai függenek a kezdeti
perturbációktól. A hőmérsékleti fluktuációra vonatkozó (6.121)-(6.124) Boltzmann-egyenlet
multipólus-komponensek azonban
nem függnek expliciten
![]() -tól, ezért
-tól, ezért
![]() csupán időtől független szorzóban tartalmazhat
csupán időtől független szorzóban tartalmazhat
![]() -függést:
-függést:
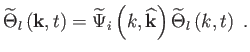 |
(6.132) |
A gravitációs potenciál perturbációja szintén Gauss-eloszlást
követő homogén és izotrop valószínűségi mező. A 2-pont-korrelációs
függvényének
Fourier-transzformáltja adja a
![]() kezdeti teljesítményspektrumot. A homogenitás és izotrópia miatt a
gravitációs potenciál-perturbáció Fourier-transzformáltja
különböző hullámszámú fluktuációi közti korrelációs függvény:
kezdeti teljesítményspektrumot. A homogenitás és izotrópia miatt a
gravitációs potenciál-perturbáció Fourier-transzformáltja
különböző hullámszámú fluktuációi közti korrelációs függvény:
Felhasználva
![]() Fourier-transzformáltjának
Legendre-polinomok szerinti kifejtését, a gömbfüggvények addíciós
tételét és (6.131) összefüggést, a
szög-teljesítményspektrum kifejezhető
a
Fourier-transzformáltjának
Legendre-polinomok szerinti kifejtését, a gömbfüggvények addíciós
tételét és (6.131) összefüggést, a
szög-teljesítményspektrum kifejezhető
a
![]() anizotrópia-momentumokkal és a
anizotrópia-momentumokkal és a
![]() kezdeti teljesítményspektrummal [37]:6.16
kezdeti teljesítményspektrummal [37]:6.16
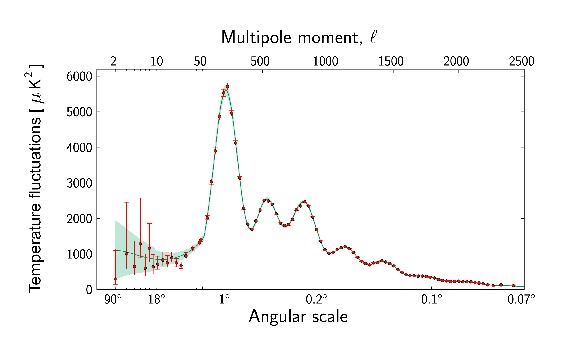 |
A teljesítményspektrum meghatározásában fontos szerepe volt a WMAP
űrszondának, valamint értékes kiegészítéseket adtak a South Pole
Telescope mérései
is [43]. A jelenleg
rendelkezésre álló legpontosabb hőmérsékleti
teljesítményspektrumot a 6.21 ábra
mutatja be ([44] 37.
ábrája). Látható, hogy a modell és a megfigyelések igen
pontosan illeszkednek ![]() tartományban, azonban nagy szögskálákon
(kis
tartományban, azonban nagy szögskálákon
(kis ![]() -ekre)
egyrészt a hibahatárok nagyok, másrészt túl sok pont került a
modell által jósolt görbe alá. Az eltérés okait jelenleg
vizsgálják. A
Planck szonda adataiból készített teljesítményspektrum 7 csúcsot
tartalmaz,
szemben a WMAP által azonosított 4 csúccsal, így a kozmológiai
paraméterek
pontosabban határozhatók meg.
-ekre)
egyrészt a hibahatárok nagyok, másrészt túl sok pont került a
modell által jósolt görbe alá. Az eltérés okait jelenleg
vizsgálják. A
Planck szonda adataiból készített teljesítményspektrum 7 csúcsot
tartalmaz,
szemben a WMAP által azonosított 4 csúccsal, így a kozmológiai
paraméterek
pontosabban határozhatók meg.
Szeged 2013-05-01